For any musician who's spent a lifetime practicing learning your craft, this might not be something that you'll want to read. Forbes recently compiled a list of
the world's top 10 money making DJ's. While still not as much as the
current pop stars, some DJ's are sure raking in a lot of cash, but
that's thanks to a global EDM industry that is now worth an estimated $4
billion.
Here's the list:
1. Tiesto - $22 million
2. Skrillex - $15 million
3. Swedish House Mafia - $14 million
4. David Guetta - $13.5 million
5. Steve Aoki - $12 million
6. Deadmau5 - $11.5 million
7. DJ Pauly D - $11 million
8. Kadkade - $10 million
9. Afrojack - $9 million
10. Avicii - $7 million
Keep in mind that their income is from touring (Tiesto makes about $250k a night), endorsements, and merch.
Wednesday, August 8, 2012
Introduction to Digital Audio
Digital audio at it’s most fundamental level is a mathematical representation of a continuous sound.
The digital world can get complicated very quickly, so it’s no surprise that a great deal of confusion exists.
The point of this article is to clarify how digital audio works without delving fully into the mathematics, but without skirting any information.
The key to understanding digital audio is to remember that what’s in the computer isn’t sound – it’s math.
What Is Sound?
Sound is the vibration of molecules. Mathematically, sound can accurately be described as a “wave” – meaning it has a peak part (a pushing stage) and a trough part (a pulling stage).
If you have ever seen a graph of a sound wave it’s always represented as a curve of some sort above a 0 axis, followed by a curve below the 0 axis.
What this means is that sound is “periodic.” All sound waves have at least one push and one pull – a positive curve and negative curve. That’s called a cycle. So – fundamental concept – all sound waves contain at least one cycle.
The next important idea is that any periodic function can be mathematically represented by a series of sine waves. In other words, the most complicated sound is really just a large mesh of sinusoidal sound (or pure tones). A voice may be constantly changing in volume and pitch, but at any given moment the sound you are hearing is a part of some collection of pure sine tones.
Lastly, and this part has been debated to a certain extent – people do not hear higher pitches than 22 kHz. So, any tones above 22 kHz are not necessary to record..
So, our main ideas so far are:
—Sound waves are periodic and can therefore be described as a bunch of sine waves,
—Any waves over 22 kHz are not necessary because we can’t hear them.
How To Get From Analog To Digital
Let’s say I’m talking into a microphone. The microphone turns my acoustic voice into a continuous electric current. That electric current travels down a wire into some kind of amplifier then keeps going until it hits an analog to digital converter.
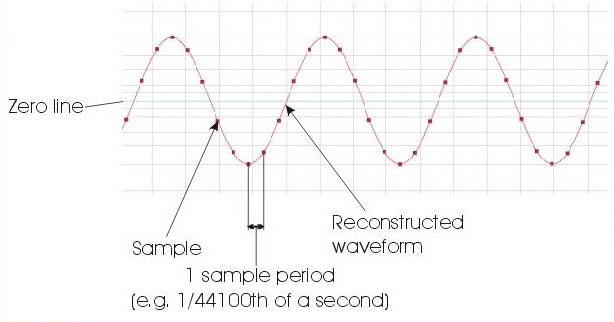
Remember that computers don’t store sound, they store math, so we need something that can turn our analog signal into a series of 1s and 0s. That’s what the converter does. Basically it’s taking very fast snapshots, called samples, and giving each sample a value of amplitude.
This gives us two basic values to plot our points – one is time, and the other is amplitude.
Resolution & Bit Depth
Nothing is continuous inside the digital world – everything is assigned specific mathematical values.
In an analog signal a sound wave will reach it’s peak amplitude – and all values of sound level from 0db to peak db will exist.
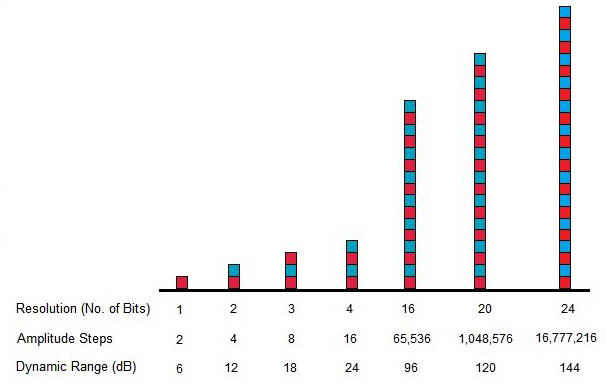
In a digital signal, only a designated number of amplitude points exist.
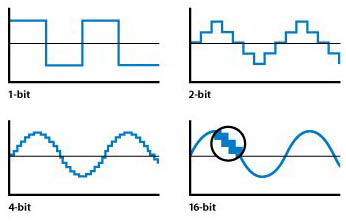
Think of an analog signal as someone going up an escalator – touching all points along the way, while digital is like going up a ladder – you are either on one rung or the next.
Let’s say you have a rung at 50, and a rung at 51. Your analog signal might have a value of 50.46 – but it has to be on one rung or the other – so it gets rounded off to rung 50. That means the actual shape of the sound is getting distorted. Since the analog signal is continuous, that means this is constantly happening during the conversion process. It’s called quantization error, and it sounds like weird noise.
But, let’s add more rungs to the ladder. Let’s say you have a rung at 50, one at 50.2, one at 50.4, one at 50.6, and so on. Your signal coming in at 50.46 is now going to get rounded off to 50.4. This is a notable improvement. It doesn’t get rid of the quantization error, but it reduces it’s impact.
Increasing the bit-depth is essentially like increasing the number of rungs on the ladder. By reducing the quantization error, you push your noise floor down.
Who cares? Well, in modern music we use a LOT of compression. It’s not uncommon to peak limit a sound, compress it, sometimes even a third hit of compression, and then compress and limit the master buss before final print.
Remember that one of the major artifacts of compression is bringing the noise floor up! Suddenly, the very quiet quantization error noise is a bit more audible. This becomes particularly noticeable at the quietest sections of the sound recording – (i.e. fades, reverb tails, and pianissimo playing.)
A higher bit depth recording will allow you to hit your converter with more headroom to spare and without compression to stay well above the noise floor.
Sampling rate is probably the area of greatest confusion in digital recording. The sample rate is how fast the computer is taking those “snapshots” of sound.
Most people feel that if you take faster snapshots (actually, they’re more like pulses than snapshots, but whatever), you will be capturing an image of the sound that is closer to “continuous.” And therefore more analog. And therefore more better. But this is in fact incorrect.
Remember, the digital world is capturing math, not sound. This gets a little tricky, but bear with me.
Sound is fundamentally a bunch of sine waves. All you need is at least three point values to determine a sine wave function that crosses all three. Two will still leave some ambiguity – but three – there’s only one curve that will work. As long as your sample rate is catching points fast enough you will grab enough data to recreate the sine waves during playback.
In other words, the sample rate has to be more than twice as fast as the speed of the sine wave in order to catch it. If we don’t hear more than 22 kHz, or sine waves that cycle 22,000 times a second, we only need to capture snapshots more than 44,000 times a second.
Hence the common sample rate: 44.1 kHz.
But wait, you say! What if the function between those three points is not a sine wave. What if the function is some crazy looking shape and it just so happens that your A/D only caught three that made it look like a sine wave?
Well, remember that if it is some crazy function, it’s really just a further combination of sine waves. If those sine waves are within the audible realm they will be caught because the samples are being grabbed fast enough. If they are too fast for the our sample rate it’s OK, because we can’t hear them.
Remember, it’s not sound, it’s math. Once the data is in, the computer will recreate a smooth continuous curve for playback, not a really fast series of samples. It doesn’t matter if you have three points or 300 along the sine curve – it’ll still come out sounding exactly the same.
So what’s up with 88.2, 96, and 192 samples/second rates?
Well, first, it’s still somewhat shaky ground as to whether or not we truly don’t perceive sound waves that are over 22 kHz.
Secondly, our A/D uses a band-limiter at the edge of 1/2 our sampling rate. At 44.1, the A/D cuts off frequencies higher than 22 kHz. If not handled properly, this can cause a distortion called “aliasing” that effects lower frequencies.
In addition, certain software plug-ins, particularly equalizers suffer from inter-modular phase distortion (yikes) in the upper frequencies. The reason being, phase distortion is a natural side effect of equalization – it occurs at the edges of the effected bands. If you are band-limited to 22 kHz and do a high end boost, the high end brickwall stops at 22 kHz.
Instead of the phase distortion occurring gradually over the sloping edge of your band, it occurs all at once in the same place. This is a subject for another article, but ultimately this leaves a more audible “cheapening” of the sound.
Theoretically a 16-bit recording at 44.1 smpl/sec will have the same fidelity as a 24-bit recording at 192. But in practicality, you will have clearer fades, clearer reverb tails, smoother high end, and less aliasing working at higher bit depths and sample rates.
The whole digital thing can be very complicated – and in fact this is only touching the surface. Hopefully this article helped to clarify things. Now go cut some records!
The digital world can get complicated very quickly, so it’s no surprise that a great deal of confusion exists.
The point of this article is to clarify how digital audio works without delving fully into the mathematics, but without skirting any information.
The key to understanding digital audio is to remember that what’s in the computer isn’t sound – it’s math.
What Is Sound?
Sound is the vibration of molecules. Mathematically, sound can accurately be described as a “wave” – meaning it has a peak part (a pushing stage) and a trough part (a pulling stage).
If you have ever seen a graph of a sound wave it’s always represented as a curve of some sort above a 0 axis, followed by a curve below the 0 axis.
What this means is that sound is “periodic.” All sound waves have at least one push and one pull – a positive curve and negative curve. That’s called a cycle. So – fundamental concept – all sound waves contain at least one cycle.
The next important idea is that any periodic function can be mathematically represented by a series of sine waves. In other words, the most complicated sound is really just a large mesh of sinusoidal sound (or pure tones). A voice may be constantly changing in volume and pitch, but at any given moment the sound you are hearing is a part of some collection of pure sine tones.
Lastly, and this part has been debated to a certain extent – people do not hear higher pitches than 22 kHz. So, any tones above 22 kHz are not necessary to record..
So, our main ideas so far are:
—Sound waves are periodic and can therefore be described as a bunch of sine waves,
—Any waves over 22 kHz are not necessary because we can’t hear them.
How To Get From Analog To Digital
Let’s say I’m talking into a microphone. The microphone turns my acoustic voice into a continuous electric current. That electric current travels down a wire into some kind of amplifier then keeps going until it hits an analog to digital converter.
Remember that computers don’t store sound, they store math, so we need something that can turn our analog signal into a series of 1s and 0s. That’s what the converter does. Basically it’s taking very fast snapshots, called samples, and giving each sample a value of amplitude.
This gives us two basic values to plot our points – one is time, and the other is amplitude.
Resolution & Bit Depth
Nothing is continuous inside the digital world – everything is assigned specific mathematical values.
In an analog signal a sound wave will reach it’s peak amplitude – and all values of sound level from 0db to peak db will exist.
In a digital signal, only a designated number of amplitude points exist.
Think of an analog signal as someone going up an escalator – touching all points along the way, while digital is like going up a ladder – you are either on one rung or the next.
Let’s say you have a rung at 50, and a rung at 51. Your analog signal might have a value of 50.46 – but it has to be on one rung or the other – so it gets rounded off to rung 50. That means the actual shape of the sound is getting distorted. Since the analog signal is continuous, that means this is constantly happening during the conversion process. It’s called quantization error, and it sounds like weird noise.
But, let’s add more rungs to the ladder. Let’s say you have a rung at 50, one at 50.2, one at 50.4, one at 50.6, and so on. Your signal coming in at 50.46 is now going to get rounded off to 50.4. This is a notable improvement. It doesn’t get rid of the quantization error, but it reduces it’s impact.
Increasing the bit-depth is essentially like increasing the number of rungs on the ladder. By reducing the quantization error, you push your noise floor down.
Who cares? Well, in modern music we use a LOT of compression. It’s not uncommon to peak limit a sound, compress it, sometimes even a third hit of compression, and then compress and limit the master buss before final print.
Remember that one of the major artifacts of compression is bringing the noise floor up! Suddenly, the very quiet quantization error noise is a bit more audible. This becomes particularly noticeable at the quietest sections of the sound recording – (i.e. fades, reverb tails, and pianissimo playing.)
A higher bit depth recording will allow you to hit your converter with more headroom to spare and without compression to stay well above the noise floor.
Sampling rate is probably the area of greatest confusion in digital recording. The sample rate is how fast the computer is taking those “snapshots” of sound.
Most people feel that if you take faster snapshots (actually, they’re more like pulses than snapshots, but whatever), you will be capturing an image of the sound that is closer to “continuous.” And therefore more analog. And therefore more better. But this is in fact incorrect.
Remember, the digital world is capturing math, not sound. This gets a little tricky, but bear with me.
Sound is fundamentally a bunch of sine waves. All you need is at least three point values to determine a sine wave function that crosses all three. Two will still leave some ambiguity – but three – there’s only one curve that will work. As long as your sample rate is catching points fast enough you will grab enough data to recreate the sine waves during playback.
In other words, the sample rate has to be more than twice as fast as the speed of the sine wave in order to catch it. If we don’t hear more than 22 kHz, or sine waves that cycle 22,000 times a second, we only need to capture snapshots more than 44,000 times a second.
Hence the common sample rate: 44.1 kHz.
But wait, you say! What if the function between those three points is not a sine wave. What if the function is some crazy looking shape and it just so happens that your A/D only caught three that made it look like a sine wave?
Well, remember that if it is some crazy function, it’s really just a further combination of sine waves. If those sine waves are within the audible realm they will be caught because the samples are being grabbed fast enough. If they are too fast for the our sample rate it’s OK, because we can’t hear them.
Remember, it’s not sound, it’s math. Once the data is in, the computer will recreate a smooth continuous curve for playback, not a really fast series of samples. It doesn’t matter if you have three points or 300 along the sine curve – it’ll still come out sounding exactly the same.
So what’s up with 88.2, 96, and 192 samples/second rates?
Well, first, it’s still somewhat shaky ground as to whether or not we truly don’t perceive sound waves that are over 22 kHz.
Secondly, our A/D uses a band-limiter at the edge of 1/2 our sampling rate. At 44.1, the A/D cuts off frequencies higher than 22 kHz. If not handled properly, this can cause a distortion called “aliasing” that effects lower frequencies.
In addition, certain software plug-ins, particularly equalizers suffer from inter-modular phase distortion (yikes) in the upper frequencies. The reason being, phase distortion is a natural side effect of equalization – it occurs at the edges of the effected bands. If you are band-limited to 22 kHz and do a high end boost, the high end brickwall stops at 22 kHz.
Instead of the phase distortion occurring gradually over the sloping edge of your band, it occurs all at once in the same place. This is a subject for another article, but ultimately this leaves a more audible “cheapening” of the sound.
Theoretically a 16-bit recording at 44.1 smpl/sec will have the same fidelity as a 24-bit recording at 192. But in practicality, you will have clearer fades, clearer reverb tails, smoother high end, and less aliasing working at higher bit depths and sample rates.
The whole digital thing can be very complicated – and in fact this is only touching the surface. Hopefully this article helped to clarify things. Now go cut some records!
Subscribe to:
Posts (Atom)